На самом деле, данная запись несёт ту же цель, что и предыдущая, то есть говорит о том, как можно легко запомнить то, что большинство людей очень быстро забывает. Так вот, большинство из нас как раз не могут запомнить ту однообразно-запутанную формулу для векторного произведения. Это вам не скалярное произведение векторов, и даже не умножение на константу, это векторное произведение!
Итак, ещё где-то на первом (или втором?) курсах большинства второсортных ВУЗов бедным студентам давали формулу, которую предлагалось тупо запомнить. Мне повезло больше (в плане преподавателя), он мимолётом упомянул, как эта формула вообще получается. С этого момента всё встало на свои места, и хотя я редко умножаю вектора векторно, формулу я запомнил навсегда. Я думаю, что сейчас её также хорошо запомнят и все те, кто хотя бы знает, как находить определитель третьего порядка. В конце этой записи вы как раз и увидите ту формулу, о которой я говорил, поэтому в начале я её приводить не буду, а только классифицирую проблему:
- направление результирующего вектора каждый более-менее сообразительный физик ещё как-то сможет определить (оно перпендикулярно исходным векторам и при этом образует с ними правую тройку, то есть расположено по правилу буравчика или правого винта), а вот координаты этого вектора — уже не каждый…
- общий вид формулы помнят многие, однако немногие в нём не путаются: чаще всего путают порядок чередования индексов (1, 2, 3) с обозначениями компонентов (x, y, z), реже путают местами сомножители из разных слагаемых…
Я уже сказал в начале, что проще всего будет сейчас тем, кто умеет находить определители третьего порядка (лучше всего разложением по первой строке):
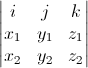в первой строчке находятся единичные векторы-орты, они там находятся всегда и не важно, какие координаты у самих перемножаемых векторов; а вот координаты этих векторов расположены во второй и третьей строчках:
- во второй строке координаты того вектора, который мы умножаем
- в третьей строчке координаты того, накоторый умножаем
Вы же помните, что здесь от перестановки мест сомножителей произведение поменяется?
Итак, мы выяснили, что в первой строчке единичные орты, во второй — вектор с координатами (x1, y1, z1), а в третьей — координаты вектора с координатами (x2, y2, z2). Считать определитель можете как хотите, а я разложу его по первой строке:
теперь раскрою определители второго порядка (перемножу их компоненты крест-накрест и вычту):
а теперь внесу знак «минус» перед второй скобкой внутрь неё:
как вы уже догадались, в скобках у нас и оказались компоненты вектора, получающегося в результате векторного произведения, то есть:
Таким образом, все три координаты вектора выглядят вот так:
Мораль: линейную алгебру знать всё же нужно. Как видите, она необходима даже в геометрии со всеми вытекающими отсюда последствиями.