Эту задачу я как-то давно нашёл в учебнике по дифференциальным уравнениям в разделе «Для самостоятельного решения». На тот момент мне она показалась сложной, но почему-то я её очень хорошо запомнил. Пытался решить её неоднократно. Через месяц ещё, потом ещё и ещё. Наконец, примерно через год (точнее затрудняюсь сказать) шёл по улице и вдруг меня осенила простая идея. Задачу я всё-таки решил, но не при помощи ДУ, а составив простенький ряд, который сходится к ответу. Может быть кто-то мне подскажет, как решить эту задачу всё-таки с помощью дифференциального уравнения?
Сложность как раз и состоит в том, что я даже не могу сформулировать эту задачу на языке дифференциального исчисления. Поэтому даже не встаёт вопрос: «Как решать это уравнение?». Итак, для начала сформулируем задачу на человеческом языке:
В вершинах равностороннего треугольника со стороной L расположены три черепахи, пронумерованные по порядку (1, 2, 3). В начальный момент времени они одновременно начинают движение, оно равномерное, скорость у всех черепах одинаковая по величине. Черепаха №1 движется строго в направлении черепахи №2. Черепаха №2 строго движется по направлению к черепахе №3. Черепаха №3 движется строго к черепахе №1. Учтите, что черепахи всегда движутся только в направлении другой черепахи. Найти путь, пройденный каждой черепахой к моменту, когда они встретятся в одной точке.
Вот, собственно, и всё. Движение черепах (траектория) чем-то напоминает спираль. И вот длину этой спирали и нужно посчитать. В дифференциальном отношении, возможно, нужно поставить зависимость векторов скоростей по времени, при этом учесть, что скорости постоянные по модулю, но переменные по направлению.
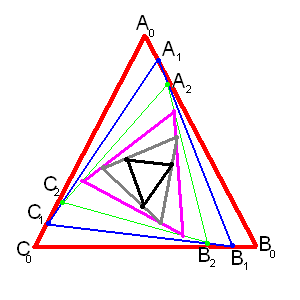
А на рисунке я попробовал с помощью дополнительного построения проиллюстрировать то, как решил эту задачу я сам. Допустим, первая черепаха находится в нулевой точке А. В этот момент черепаха №2 находится в нулевой точке В. В бесконечно малый промежуток времени черепаха №1 переместится в точку, близкую к первой точке А, а вторая — во первую точку В (движение третьей черепахи я описывать не буду — оно аналогично). Из-за малости промежутка времени их перемещение тоже окажется бесконечно малым и отклонением отрезков А0-А1 от А0-В0 (и соответственно В0-В1 от В0-С0) можно пренебречь. На полученных новых точках (А1, В1, С1) построим новый треугольник (он выделен синим цветом). И вот на этом моменте уже перестанем пренебрегать отклонением перечисленных выше отрезков от базовых линий (выделены красным). Черепахи к этому времени продолжают движения из вершин нового треугольника и за второй бесконечно малый промежуток времени передвинутся в точки А2, В2, С2, на которых мы снова построим новый треугольник (выделен зелёным цветом). Своё движение черепахи продолжат уже по нему. Затем они будут двигаться по линиям розового треугольника, потом серого, а потом чёрного. На каждой подобной итерации промежуток времени подбирается такой, чтобы отклонением от спирали действительно можно было пренебречь. Таких треугольников, соответственно, будет много. Если же мы устремим это число в бесконечность, то как раз и получим реальную траекторию движения черепах. Теперь найдём пройденный ими путь (для примера возьмём только первую черепаху):
S = A0A1 + A1A2 + … + An-1An = (A0B0 — A1B0) + (A1B1 — A2B1) + … (An-1Bn-1 — AnBn-1)
Теперь осталось раскрыть скобки и учесть малые отклонения между сторонами треугольников на соседних итерациях. Это означает, что треугольник на 10-й итерации практически равен треугольнику на 11-й итерации, то есть их стороны между собой приблизительно равны (*). Учитывая при этом, что на каждой новой итерации сторона всё-таки чуток меньше, чем предыдущая, то при бесконечном числе итераций последняя сторона последнего треугольника станет нулевой, бесконечно малой (**). Учитывая утверждения (*) и (**) можно сказать, что A1B0 примерно равен A1B1 и их можно сократить (при раскрытии скобок у них получились противоположные знаки). Аналогично поступим и с другими слагаемыми вида AnBn-1 , AnBn. В итоге у нас сокращаются все слагаемые, кроме первого.
Ответ — путь черепахи при любой скорости будет равен L, то есть стороне исходного треугольника. Это верно тогда и только тогда, когда все черепахи двигаются с одинаковой по модулю скоростью и двигаются строго по направлению друг к другу.

где то в ваших размышлениях ошибка, так как точное кинематическое решение дает путь 2·l / 3 , где l сторона треугольника
Да я, если честно, уже давно сам засомневался в верности. И, в общем-то, уже понял, что у меня идёт накопление ошибки на каждой итерации. В итоге, я снова в раздумьях… Хочется красивого решения ещё.